2018-10-08

Parking Lot Gate Brute Force Scanner

My apartment building has a remote-controlled gate to the parking lot. The remote has a secret 10-bit key encoded in it for security.

Recently my remote broke and in replacing it I thought about how hard it would be to make my own remote. I also wondered what it would take to brute-force guess all the keys.

In the end, I built a multi-function gate remote which can:

Open my gate
Open any gate of this kind (brute-force guessing)
Keep the gate open all the time
Keep the gate closed all the time

Technologies

Microcontroller

RF Module (RF4463PRO)

Audacity (audio editor)

SDR# (RF spectrum analyzer)

Radio-controlled gate

Research and Build

How it works in the first place

Remote controlled gates have a computer system attached which:

Listens for signals from remotes
Compares against the pre-configured secret 10-bit key

Here is my gate:

You can see the radio antenna leading to the control system operating the gate.

The remotes for these types of gates look like this, which is a Stanley 1050 controller operating at 310MHz.

Inside the remote is a 10-bit DIP switch indicating what code the remote should send. If this matches the gate control system, the gate should open.

(Also yes this is my gate combination, I’m not super worried about it)

Going deeper, how does the RF modulation work?

In order to understand how to make a replacement remote I had to figure out how this one worked in the first place.

Clearly it’s radio at 310MHz, but what was the encoding scheme for transmitting the 10-bit key?

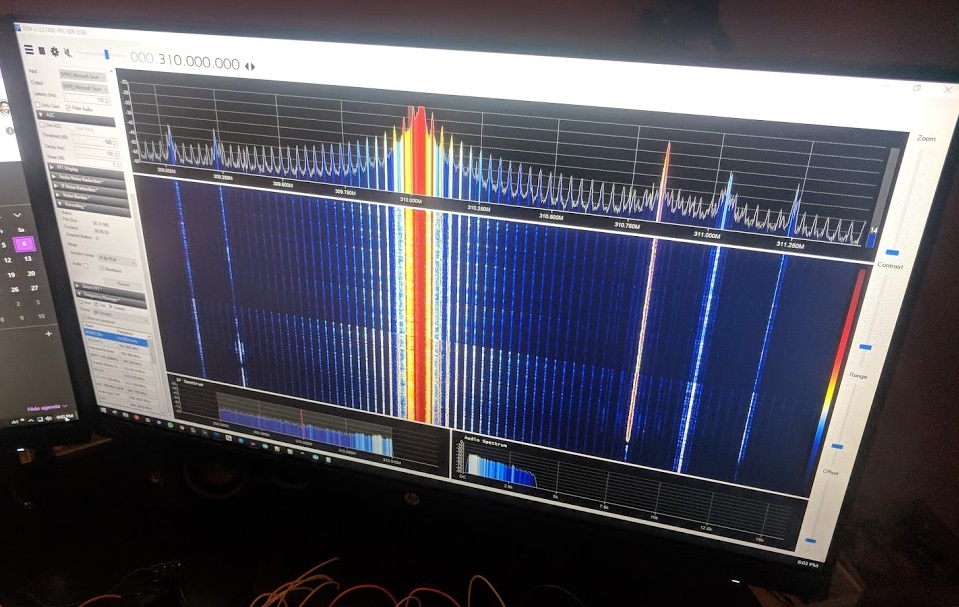
Using SDR# and a software defined radio (SDR), I was able to snoop the radio transmissions. The data is stored in an audio file.

Here is the SDR interface while I was recording:

I was able to open the resulting audio file in Audacity and zoom in on the patterns seen.

In my analysis, we’re seeing:

ASK modulation (amplitude shift keying, which is basically on/off keying)
10-bit number (as expected)
Bit duration of 1.96 milliseconds
- High bit duration of 1.48 milliseconds
- Low bit duration of 0.49 milliseconds
Total duration to send one complete 10-bit code of 19.6 milliseconds
Spacing of 20 milliseconds between repeated transmissions (if you hold the button down)

Can I build it myself?

So provided I could reproduce in RF the code with those timings, it should work.

Since I had the RF modules from my balloon flights I was able to modify my libraries to support ASK modulation and get a prototype working without too much pain.

After putting together a rough outline of the controller code, it worked! I can open the gate!

Can I brute-force guess the 10-bit key?

Yes in theory, just start with the 10-bit code of all 0, then add 1, try it, and so on.

The remote wouldn’t know if it hit on the right code, but the gate would open and that’s all you’d really care about.

At 20 milliseconds code length, and 20 milliseconds spacing, and 1024 combinations, you’re looking at (20+20)*1024 milliseconds, which is about 40 seconds total duration.

Sadly, my gate doesn’t seem to open the first time it receives the correct code. It forces you to hold the button for a moment and get several correct codes in a row.

In fact, it takes 5 consecutive correct codes before the gate opens.

This puts the total guess time to 3 minutes and 20 seconds. It’s a bit on the slow side but as a proof of concept very acceptable!

Here is the moment of truth:

Can I speed up the brute-force?

Yes, there are ways to do this that work in theory, but don’t work with my specific gate.

The concept is basically to assume the gate has a shift-register-like device checking for the right code.

Think of an ATM password, which is 3456.

If I want to brute force it, at some point I’m going to try 2345, and later get to 3456. Those two tries will each take the same duration, adding up to be 8x single-digit duration.

If I want to improve on 8x, consider what happens if I tried pressing keys 23456. The sequence 2345 is in there, and so is 3456. This whole sequence would take 5x single-digit duration, which is a big improvement over 8x.

ATMs, of course, don’t work this way, but according to some articles I was able to find on the internet, some gates do.

Sadly, my gate is fussy and wants the right sequence 5 times in a row before opening, which rules out using the procedure above directly.

I did try the approach though.

It requires determining the “shortest superstring” of all the 10-bit numbers, meaning each 10-bit number shows up in its entirety somewhere in the superstring. And clearly they aren’t going to be in sequential order.

I followed the approach described here (link).

I pre-calculated the value on a regular PC instead of in the remote-control microcontroller.

The shortest sequence would be 1,066 digits. Compare that to the 10,240 the sequential brute-force attempt takes. That’s a 90% savings!

Here is the sequence generated if you’re wondering:

10101010011010101001000001111000001001100000101010000010001000001011111111000000
10110000001101000000100100000011100000001010000000110000000011111111110111000001
10010000000000100000000011100110001011010111101010000111001100001110101001011110
11101000001101111111001111000101111000011110100001011011011000011000100011111100
01111101100000111011111000100001111100001001010000100001001111111010101010001000
10100010101010110000100011000010100100001010110010001001001000101100101101000011
00110000101011011001010110100011001111101001001111001001110110001010111111010001
11101111110010101001001011100111010110101001111011011010101101001011001110000110
10100011101101111010011011001111010110011010001011101100100110011011101101001100
01111001101101110101111101011101110111100111001111110110101100010010110111110111
10110011001010010100110010010101011100001011100010011010010001110010000110110001
10001101110001100101110100101011101010111100101111100100011010011101000100111000
10100111001011000111000111010011111001100111011100110101101110010010011011110001
10101110010100011011010001